哈夫曼树
哈夫曼树的基本概念与结构:
1、哈夫曼树的概念:
哈夫曼树又叫最优二叉树,是一种带权路径长度最短的二叉树。
· 路径:从一个节点到另一个节点时,中间经过的所有节点即为两节点之间的路径。
· 路径长度:路径上的分支数目(“边”的数目)即为路径的长度。
· 树的路径长度:从根节点到每个节点之间的路径长度之和。
· 节点的权:将树中的节点赋予一个某个含义的数值作为该节点的权值,该值为节点的权。
· 带权路径长度:从根节点到某个节点之间的路径长度与该节点的权的乘积。
· 树的带权路径长度:所有叶子节点的带权路径长度之和,称为WPL。而带权路径长度最短的就是哈夫曼树。
2、哈夫曼树的节点结构:
struct node
{
int key; // 节点的权值
struct node *left; // 左孩子节点,左子树
struct node *right; // 右孩子节点,右子树
};
void destory(struct node *tree); //删除树
struct node *createHuff( int *parr, int size ); //创建哈夫曼树节点
void inorder(struct node *tree); //中序递归遍历哈夫曼树
void preOrderTraverse(struct node *tree); //先序递归遍历哈夫曼树
void posorder(struct node *tree); //后序递归遍历哈夫曼树
void findNode(struct node *tree); //哈夫曼树查找
struct node *findHuff(struct node *tree, int val, int *pos); //查找哈夫曼树父亲节点
struct node *delHuff(struct node *root, int val); //删除指定节点
void showHuff( struct node*tree ); //打印哈夫曼树
3、哈夫曼树的构造步骤:
假设有n个权值,则构造出的哈夫曼树有n个叶子节点,构造过程如下:
(1)将每个权值看成具有n颗树的森林,每棵树只有一个节点。
(2)在森林中选取两个权值最小的树,分别作为左子树与右子树,构建一颗新的树。新树的权值等于左右子树权值之和。
(3)从森林中删除权值最小的树,将构建完成的新树加入森林。
(4)重复第二第三步,直到只剩一棵树,那么这棵树就是哈夫曼树。
4、哈夫曼树创建实例:
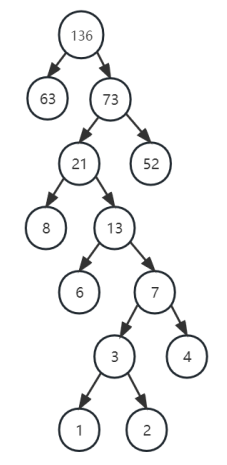
以数组{1,8,52,6,63,2,4}为例创建哈夫曼树:
(1)先将数组排序为:1,2,4,6,8,52,63。

(2)将每个权值看作一个节点,取出最小的节点。然后将其合为一个新的树,该树的根节点为左右子树权值之和。
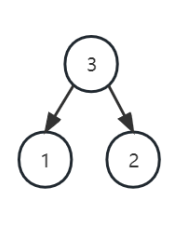
(3)将第二步中取出的节点删除,然后将新合成的节点放入序列重新排序。
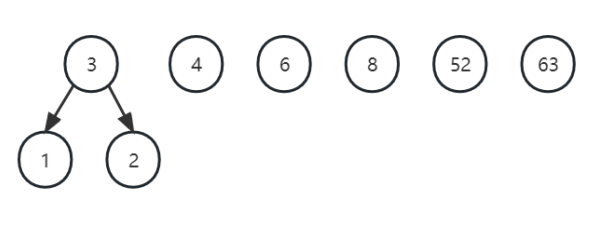
(4)按照如上步骤,不断重复执行,直到只剩一颗树。
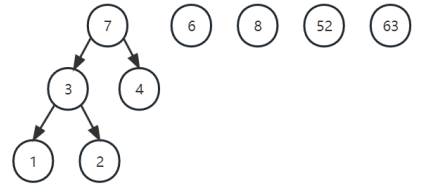
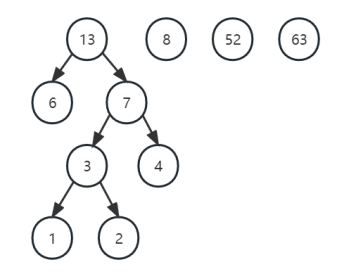
... ... 直到最后只剩一棵树时即为:哈夫曼树
5、哈夫曼树构建代码:
#include <stdio.h>
#include <stdlib.h>
struct huff
{
int key; // 权值
struct huff *left; // 左子树
struct huff *right; // 右子树
};
// 创建哈夫曼树
struct huff *createHuff( int *parr, int size )
{
int i = 0;
int j = 0;
struct huff **tree = NULL;
struct huff *root = NULL;
tree = malloc( sizeof(struct huff)*size );
// 初始化tree指针数组,使每个指针成员指向parr所指向的数组元素
for( i=0; i<size; i++ )
{
tree[i] = malloc(sizeof(struct huff));
tree[i]->key = parr[i];
tree[i]->left = NULL;
tree[i]->right = NULL;
}
// 进行size-1次循环,创建哈夫曼树
for( i=0; i<size-1; i++ )
{
// min为森林中最小权值数的根节点下标,subMin为次最小权值的下标
int min = -1;
int subMin = 0;
// 使min指向森林中的第一棵树,subMin指向第二棵树
for( j=0; j<size; j++ )
{
if( (tree[j]!=NULL) && (min==-1) )
{
min = j;
continue;
}
if( tree[j] != NULL )
{
subMin = j;
break;
}
}
// 在森林中求出最小权值树与次最小权值树
for( j=subMin; j<size; j++ )
{
if( tree[j] != NULL )
{
if( tree[j]->key < tree[min]->key )
{
subMin = min;
min = j;
}
else if( tree[j]->key < tree[subMin]->key )
{
subMin = j;
}
}
}
// 由最小权值树与次最小权值树建立一颗新树,root指向其根节点
root = malloc(sizeof(struct huff));
root->key = tree[min]->key + tree[subMin]->key;
root->left = tree[min];
root->right = tree[subMin];
tree[min] = root; // 将新树的根节点加入森林中
tree[subMin] = NULL; // 将次最小置空
}
free( tree ); // 删除动态建立的数组tree
//showHuff( root );
return root; // 返回哈夫曼树的根节点
}
// 哈夫曼树遍历
void showHuff( struct huff *tree )
{
if( tree != NULL )
{
printf( "当前节点为:%d.", tree->key );
if( tree->left != NULL )
{
printf( "它的左孩子节点为:%d.", tree->left->key );
}
else
{
printf( "它没有左孩子节点." );
}
if( tree->right != NULL )
{
printf( "它的右孩子节点为:%d.", tree->right->key );
}
else
{
printf( "它没有右孩子节点." );
}
printf( "\n" );
showHuff( tree->left );
showHuff( tree->right );
}
}
int main()
{
int arr[] = {2,3,7,9,18,25};
struct huff *tree = createHuff( arr, sizeof(arr)/sizeof(int) );
showHuff( tree );
return 0;
}



